관련글
선형회귀분석 밑바닥부터 이해하기
관련글 상관관계와 상관계수 상관관계와 상관계수 1. 들어가며 연속형 변수 x, y의 관계는 상관관계(correlation) 분석을 통해 2가지 사실을 알 수 있다. 관계의 방향 관계의 강도 보통 관계의 방향은
diseny.tistory.com
1. 기본개념
다중회귀분석은 점검해야 할 가정들이 꽤 많다. 그 중 하나가 다중공선성이다. 처음 학습하는 사람들은 모형에 투입되는 설명 변수간에 큰 상관 관계가 존재하면 회귀 모형 추정이 불안정해지므로 설명 변수의 분산팽창지수(VIF) 값 >10 이면 문제가 될 수 있으니 해당 변수를 모형에서 배제하라고 배운다. 다중공선성의 의미에 대해 조금 쉽게 다가가 보자.
2. 개념 하나씩 짚어 보기
(1) 모형을 만든다는 것의 의미
반응변수(y)와 설명변수(x1, x2)와의 관계를 설명하는 다중회귀 모형(선형 모형의 경우)을 만든다는 것은
y = a + b1*x1 + b2*x2
라는 식을 세운다는 말이고, 구체적으로는 식을 구성하는 a, b1, b2 값을 찾는다는 것이다. 회귀 모형 추정이 잘못되었다거나 불안정하다는 말은 a, b1, b2 값을 신뢰할 수 없다, 또는 통계적 유의성이 없다는 말과 같은 뜻이다.
(2) 설명 변수간의 관계
b1, b2를 회귀 계수라고 부르는데, 다른 설명 변수들의 값이 일정한 경우(다른 변수를 통제했다는 표현을 쓰기도 한다), 변수 x 한 단위가 바뀔 때, 반응 변수 y가 변하는 정도를 의미한다. 여기서 중요한 말은 다른 설명 변수 값이 일정할 때라는 표현이다. 이런 가정하에 회귀 계수를 신뢰성 있게 추정하려면 x1, x2가 서로 상관성이 없어야 한다. 아래 <그림 1>을 보며 이해해 보자.
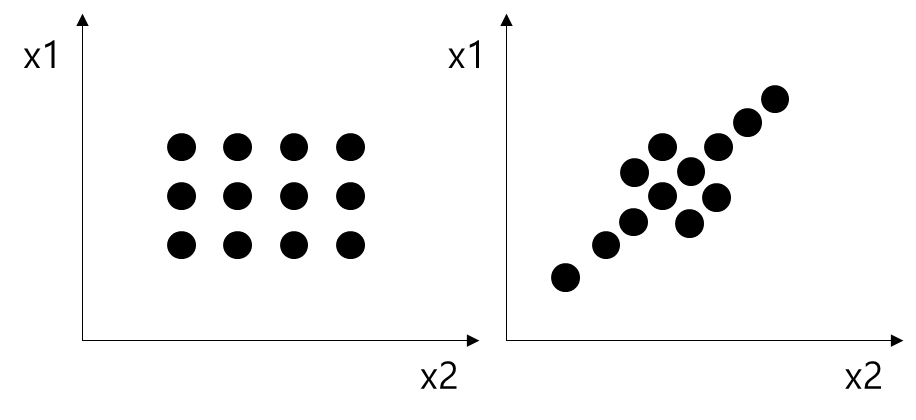
왼쪽 그림은 설명변수 x1, x2가 상관이 아주 낮은 경우인데, x1, x2가 독립적으로 변화하기 때문에 하나의 변수가 y에 미치는 순수한 영향을 추정할 수 있지만 오른쪽 그림에서는 x1, x2가 연동하기 때문에 x2가 변했을 때 y의 변화가 x2만의 순수한 효과인지 장담할 수 없다.
(3) 회귀 계수의 의미
기본적으로 다중회귀 모형의 설명 변수들은 서로 상관이 없는 것을 가정하지만 현실에서 불가능한 가정이고, 실제로는 x1, x2의 상관성을 배제하고 순수한 x1, x2가 y에 미치는 영향을 계산한 값이 다중회귀 모형의 회귀 계수다.
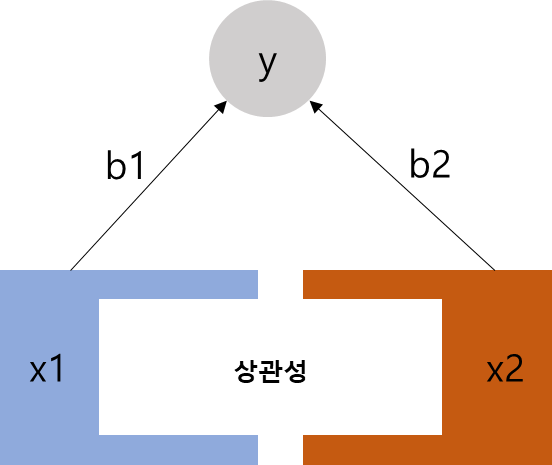
그러므로 두 변수 x1, x2의 상관성이 높으면 둘 간의 상관성을 배제한 순수한 x1, x2의 회귀계수 b1, b2의 값이 작아질 것이고, 값이 작아지면 통계적 유의성을 확보하기 어렵다.
3. 분산팽창지수(VIF)
위의 개념을 알았으면 분산팽창지수는 아주 쉽게 이해가 된다. VIF 공식은 아래와 같다.
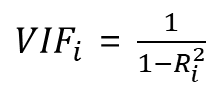
식에서 R^2(결정계수)는 하나의 설명변수를 다른 모든 설명변수로 회귀분석했을 때 얻는 값이다. 따라서 설명변수간의 연관성이 높을 수록 R^2가 커지고, 결과적으로 VIF도 커진다. VIF 값이 10이라는 것은 하나의 설명 변수에 대한 분산의 90%가 다른 모든 설명변수에 의해 설명될 때다. 즉 R^2 = 0.9인 경우이다. 그러므로 VIF가 10이상이면 거의 하나의 독립적인 변수로서의 역할을 하기 어렵다고 판단할 수 있다.
관련글
R 다중공선성 VIF 값 계산
관련글 다중공선성(Multicollinearity)의 의미와 판별법 1. 들어가며 관련글에서 다중공선성에 대한 이론적인 내용을 소개했으므로 이제 R을 이용해 VIF(분산팽창지수)를 계산하는 방법을 살펴보자. 2.
diseny.tistory.com
'통계 이론' 카테고리의 다른 글
| 가설검증과 2종오류 (0) | 2022.03.06 |
|---|---|
| 분산으로 평균차이 검증하기(분산분석) (2) | 2022.03.02 |
| 가설검증과 1종 오류 (0) | 2022.02.24 |
| 효과 크기(Effect Size)의 의미와 필요성 (2) | 2022.02.14 |
| 자유도(Degree of Freedom)에서 자유로워 지기 (6) | 2022.02.06 |
| 제곱합(Sum of Squares : SS) 공식 (0) | 2022.02.01 |
| 다중회귀 분석에서 상호작용의 의미 (5) | 2022.01.31 |




댓글