관련글
탐색적 요인분석(EFA : Exploratory Factor Analysis)
1. 기본개념 사회과학이나 심리학에서는 직접적으로 측정할 수 없는 변수를 잠재 변수(latent variable), 요인(factor), 구인(construct), 구성 개념 등으로 부른다. 데이터 분석 측면에서 보자면 보통 어떤
diseny.tistory.com
1. 데이터 생성
아래의 코드로 샘플 데이터 프레임을 생성한다.
A = c(87, 55, 81, 42, 45, 54)
B = c(92, 72, 95, 55, 87, 66)
C = c(67, 82, 38, 55, 50, 82)
D = c(40, 88, 35, 39, 57, 80)
E = c(50, 88, 45, 50, 62, 90)
color = data.frame(A, B, C, D, E)
View(color)
다음과 같이 데이터 프레임이 생성되었다.

2. 요인분석 코드
요인 수를 결정하는 방법은 여러가지가 있는데 변수들간의 상관계수 행렬에서 구한 고윳값(eigenvalue)이 1이상인 값의 수(카이저 규칙)와 스크리 도표를 이용하는 방법을 소개한다. 요인 수를 결정하는 방법은 위의 관련글을 참고하길.
(1) 고윳값 > 1 이상인 수로 결정하는 방법
cor_r = cor(color) #변수들의 상관계수
eigen_v = eigen(cor_r) #고윳값 분해
round(eigen_v$values,3)결과를 확인하면 다음과 같은 내용을 출력한다.
[1] 3.301 1.216 0.414 0.060 0.008
1이상인 값이 2개(3.301, 1,216) 있으므로 요인수를 2로 결정할 수 있다.
(2) 스크리 도표로 결정하는 방법
스크리 도표를 그리는 패키지는 많은데 2가지 방법을 소개한다. 먼저 psych 패키지를 이용하는 경우다.
library(psych) #요인분석을 위해 필요한 psych 패키지 로드
VSS.scree(color) # 스크리 도표 그리기
아래와 같은 그래프를 생성한다. 스크리 도표에서도 요인 수는 2가 적당해 보인다.

다음은 hemp 패키지를 이용하는 경우다. 마찬가지로 비슷한 스크리 도표를 출력한다.
library(hemp)
lattice_scree(color)

일반적으로 요인 수는 카이저 규칙과 스크리 도표를 모두 참고해 결정한다. 예제 데이터에서는 두 기준 모두 요인수 2가 적당하다는 결과가 나왔다.
3. 요인분석 결과 해석
이제 요인수가 2로 결정되었으니 탐색적 요인 분석을 실행해보자
color.factor = factanal(color, factors = 2) # 요인수(factors) 2로 세팅
color.factor
분석 결과는 아래와 같다.

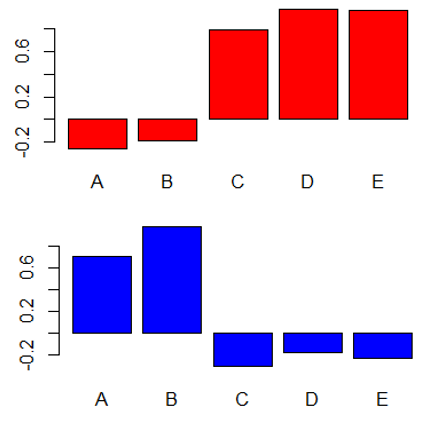
① A, B는 요인2, C, D, E는 요인1로 묶이는 것을 알 수 있다.
② 요인1이 전체 분산의 0.524, (요인1+ 요인2)이 전체 분산의 0.851을 설명하고 있다
③ 요인구조 모형 적합도는 양호하다(p < 0.05이면 부적합)
요인분석 결과 값을 막대 그래프로 그려보면 Red, Blue 요인으로 나뉜다는 것을 알 수 있다.
barplot(color.factor$loading[ ,1], col = "red") #첫번째 요인부하량 값 막대그래프로
barplot(color.factor$loading[ ,2], col = "blue") #두번째 요인부하량 값 막대그래프로
4. 요인분석 회전방법 변환
factanal 함수는 기본적으로 요인 회전 방법으로 varimax(직각 회전) 방법을 이용하는데 위의 예제에서는 요인1과 요인2가 분명하게 구분되었지만 애매하게 구분되는 경우도 있다. 이런 경우에는 요인 회전 방법을 oblimin(사각 회전) 방법을 이용하면 더 요인구조가 더 분명해질 수도 있다. GPArotation 패키지를 이용한다.
library(GPArotation)
oblimin(loadings(color.factor))결과는 아래와 같다. AB/CDE가 위의 varimax 방법보다 더 분명해지는 것을 볼 수 있다.

관련글
R 주성분 분석
1. 들어가며 주성분 분석(PCA : Principal Component Analysis)은 데이터에 변수가 많을 때 변수의 수를 축약하는 방법이다. <그림 1>은 세 개의 데이터를 x축(공부시간), y축(성적)으로 표현한 그래프다. 세
diseny.tistory.com
'R_데이터 분석 기술' 카테고리의 다른 글
| R 다중공선성 VIF 값 계산 (0) | 2022.04.04 |
|---|---|
| wide & long 데이터 형태 전환 (0) | 2022.04.04 |
| R을 이용해 상관계수 구하기 (0) | 2022.04.01 |
| 데이터 결합(join) by dplyr 패키지 (0) | 2022.04.01 |
| 변수별 부분 집계 by dplyr (0) | 2022.03.31 |
| R 전처리 최강자 dplyr 패키지 (0) | 2022.03.31 |
| 범주별 다변수 통계량 계산(by 함수) (0) | 2022.03.03 |




댓글