데이터 분석에서는 여러 그룹을 비교하거나 변수들 간의 관계를 파악하고 통계학에서는 분석을 통해 얻은 가설의 일반화 가능성을 검토한다고 설명했습니다.
반면 머신러닝(Machine Learning)은 새로운 데이터를 예측하거나 분류하는 것이 주목적입니다. 먼저 현재 보유하고 있는 데이터를 이용해 모델을 만듭니다. 그런 다음 새로운 데이터를 모델에 투입하면 모델이 목적에 맞게 예측하거나 분류합니다.

:: 참고 ::
앞으로 모델이라는 말을 자주 접하게 될 것입니다. 모델은 어떤 입력 값을 받아 특정한 방식으로 계산한 결과를 출력하는 수식, 함수, 또는 여러 단계로 구성된 절차(알고리즘)를 의미합니다. 그런 의미에서 아주 간단한 수식 y=ax+b도 모델이라고 부를 수 있습니다.
실생활에서 머신러닝을 가장 생생하게 경험할 수 있는 사례가 인터넷 쇼핑몰입니다. 대부분의 쇼핑몰은 고객이 로그인하면 관심을 가질만한 상품을 추천합니다. 상품을 추천한다는 말 자체가 로그인한 고객이 어떤 제품에 관심 있을지 예측한다는 의미입니다. 인터넷 쇼핑몰은 고객들의 구매 데이터를 쌓아 두고 그 데이터를 이용해 예측 모델을 만듭니다. 그리고 새로운 고객이 로그인하면 해당 고객에 관한 데이터(그 동안 구매한 제품, 구매 금액, 연령, 거주지 등)를 모델에 투입하고 추천할 상품을 예측합니다. 인터넷 쇼핑몰을 병원으로 바꿔서 생각한다면 암 검사를 받은 사람이 암환자인지 아닌지 분류할 수 있습니다.
중요한 사실은 머신러닝을 구성하는 주요한 이론은 거의 모두 통계학에서 시작되었다는 것입니다. 예를 들어 100명의 나이와 혈압을 측정하고 X축이 나이, Y축이 혈압인 2차원 좌표에 표시했다고 합시다. 통계학에서는 나이와 혈압의 관례를 설명하는 y=ax+b 라는 회귀식을 만들 수 있습니다.
마찬가지로 머신러닝에서도 동일하게 y=ax+b 라는 회귀모델을 만들 수 있습니다. 회귀식이나 회귀모델은 본질적으로 동일한 용어입니다. 각 분야에서 익숙하게 사용하는 표현이 다를 뿐입니다. 그림 1-5를 보면 동일한 데이터를 두고 통계학에서도 머신러닝에서도 얼핏 보면 동일한 회귀 모델을 만듭니다.

그런데 같은 y=ax+b에 대해 통계학과 머신러닝에서 관심을 갖는 부분이 조금 다릅니다. 그림 1-6처럼 통계학에서는 주어진 “데이터에 가장 잘 적합(fitted)하는” 선(모델)을 그어 a와 b를 구합니다. 데이터에 가장 잘 적합한다(데이터에 잘 맞다)는 표현은 다른 말로 주어진 데이터를 가장 잘 설명한다는 말과 같습니다. 데이터를 설명한다는 말은 X(나이)와 Y(혈압)의 관계를 잘 표현한다는 말로 다시 바꿀 수 있습니다.
이제 a와 b를 알면 1살 증가할 때 혈압이 얼마나 상승하는지 설명할 수 있습니다. y=ax+b는 x=1일 때 y=a+b, x=2일 때 y=2a+b입니다.나이)가 1 증가하면 y(혈압)는 (2a+b) – (a+b)이므로 a 만큼 증가하는 관계를 설명할 수 있는 것이죠. X가 1이 증가했을 때 정확하게 Y가 무엇인지 예측하는 것보다는 얼마나 Y를 증가시키느냐에 관심을 둡니다. 어떤 영역에서는 결과보다 결과가 도출된 과정이 더 중요할 수 있습니다.

여기서 통계학은 표본에서 얻은 결론을 일반화할 수 있는지 검증한다는 사실을 상기합시다.
쉽게 말하면 표본 데이터는 y=ax+b 라고 설명할 수 있는데, 알 수 없는 전체 데이터에서도 y=ax+b 일까? 라는 의문을 검증해야 합니다.
극단적인 예로서 그림 1-7과 같이 전체 데이터에서 x, y는 아무런 관계가 없지만 우연히 추출된 표본 데이터(빨간색 점)에서는 y=ax+b 같이 보일 수도 있습니다. 실제로 전체 데이터에서의 x와 y의 관계가 표본 데이터에서의 관계와 다를 수 있는 것이죠. 이렇듯 통계학에서는 주어진 데이터를 잘 설명하는 모델을 만들고 그 모델을 일반화할 수 있을지 검증하는 단계로 진행합니다.

한편, 머신러닝은 x에 어떤 데이터를 넣고 y를 예측하는데 관심이 있습니다.
y를 정확하게 예측하려면 당연히 모델이 x와 y의 관계를 잘 파악해야 합니다. 그러면 앞에서 살펴본 통계학적 접근법과 무슨 차이가 있을까요? 얼핏 들으면 같은 말처럼 들립니다.
여기서 예측이라는 말의 본질을 생각해 봅시다. 예측의 일반적인 의미는 새로운 데이터를 잘 맞추는 것입니다. 다음 날 축구 시합 결과를 예측한다거나 내일의 주가를 예측한다고 말할 때의 예측입니다.머신러닝에서 구축하는 모델은 x와 y의 관계를 설명하는 것보다는 예측 성능에 더 초점을 맞춥니다.
즉 모델이 더 복잡해져 x와 y의 관계를 설명하기 어려워진다고 해도 y를 더 정확하게 예측하거나 혹은 모델이 현재 데이터를 잘 설명하지 못할 만큼 단순해도 새로운 데이터를 잘 맞추는 모델을 구축합니다.
네비게이션 지도를 예로 들어 모델을 생각해 봅시다. 그림 1-9의 오른쪽 그림은 특정 공간의 실제 모습이고 왼쪽은 이 공간을 지도로 표시한 것입니다. 지도는 실제 공간을 닮은 일종의 모델입니다. 지도가 간단하게 제작될수록 이해하거나 설명하기 쉽지만 실제 공간의 모습과 점점 멀어집니다.

지도를 앞에서 설명한 수식으로 바꿔 생각해보면 y=ax+b는 간단한 모델(지도)이라 x와 y의 관계를 이해하기는 쉽지만 x와 y의 실제 관계와는 꽤 차이가 있을 수 있습니다. 아주 간단한 지도(모델)를 만들 것인지 실제와 거의 흡사한 지도를 만들 것인지는 목적에 따라 다릅니다. 예측의 정확도가 중요하다면 복잡한 모델이 필요하지만 사회 과학이나 경영 쪽에서는 예측보다는 x와 y의 관계를 잘 설명하는 것에 더 관심이 많습니다. 특정한 사회현상의 원인과 결과를 해석하기 쉬운 모델이 필요하기 때문입니다.
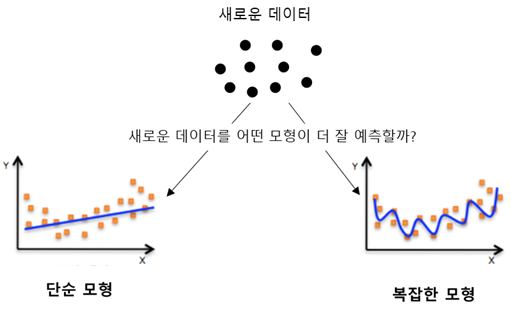
한편, 복잡한 모델을 만든다고 해서 예측력이 무한정 높아지는 것은 아닙니다. 머신러닝 모델은 마법사가 아니라 어디까지나 과거의 데이터와 패턴을 학습한 결과를 근거로 새로운 데이터나 미래를 예측하는데, 과거에 학습한 데이터와 패턴이 새롭게 발행할 수 있는 모든 데이터와 패턴을 포함하지는 않습니다.
그래서 모델이 복잡해지면 과거 데이터만 잘 학습(예측)하고 정작 미래 데이터는 제대로 예측하지 못하는 결과가 발생합니다. 따라서 예측을 잘하기 위해서는 예측력이 최대화되는 만큼만 모델이 복잡해지도록 제어할 필요가 있습니다. 이렇게 예측(또는 분류)을 잘 하도록 최적화된(적당히 복잡한) 모델을 구축하는 것이 머신러닝의 목적이라고 말할 수 있습니다.
'통계 이론' 카테고리의 다른 글
| QQ Plot 직관적으로 이해하기 (7) | 2022.01.30 |
|---|---|
| 도구의 신뢰도 측정(크론바흐 알파) (1) | 2022.01.26 |
| 탐색적 요인분석(EFA : Exploratory Factor Analysis) (0) | 2022.01.22 |
| 1. 5 데이터 과학 (0) | 2020.06.22 |
| 1.4 인공지능 (0) | 2020.06.22 |
| 1.2 통계학 (0) | 2020.06.21 |
| 1.1 데이터 분석 (0) | 2020.06.21 |



댓글