관련글
의사결정나무(decision tree)
관련글 선형회귀분석 밑바닥부터 이해하기 관련글 상관관계와 상관계수 상관관계와 상관계수 1. 들어가며 연속형 변수 x, y의 관계는 상관관계(correlation) 분석을 통해 2가지 사실을 알 수 있다.
diseny.tistory.com
1. 들어가며
R 코드를 이용해 실제로 의사결정나무분석을 해보자. 의사결정나무 알고리즘으로 irisi 데이터의 Species 범주(setosa, versicolor, virginica)를 분류한다.
2. 데이터 분할
iris 데이터를 70%의 학습데이터와 30%의 테스트 데이터로 랜덤하게 분할한다. 그런데 분할 이전에 먼저 전체 데이터에서 Species 범주에 해당하는 데이터의 비율을 확인해야 한다. 왜냐하면 임의 분할된 학습 데이터가 전체 데이터의 Species 범주 분포가 비슷한지 확인해야 하기 때문이다.
temp = table(iris$Species)
prop.table(temp)
코드를 실행해보면 각 범주가 33%씩 동일하게 분포한다는 사실을 알 수 있다. 이제 iris 데이터를 임의 분할해보자.
divide = sample(c(rep(0, 0.7 * nrow(iris)), rep(1, 0.3 * nrow(iris))))
Train = iris[divide == 0, ]
test = iris[divide == 1, ]
temp = table(Train$Species) #학습데이터의 Species 범주 분포 확인
prop.table(temp)
- ① iris 데이터 행 갯수(150개)의 70% 수 만큼 0을 생성하고, 30% 수 만큼 1을 생성한 다음 divide 벡터에 저장한다
- ② iris 데이터에서 divide 벡터가 0인 행만 추출해 Train 변수에 학습 데이터로 저장한다.
- ③ 학습데이터(Train)의 Species 범주가 전체 iris 데이터와 비슷한지 확인한다. 랜덤하게 분할되었으므로 아마 거의 비슷한 범주 분포를 보일 것이다.
3. 의사결정나무 모델 구축
library(rpart)
iris.tree = rpart(Species~., data = Train, parms = list(split = "information"))
#위 코드에서 분기점에서 변수 선택 기본값이 지니계수이므로 split = "information" 으로 엔트로피로 교체
print(iris.tree, digits = 2)
① 먼저 "library(rpart)"로 필요한 패키지를 로드한다
② rpart 함수로 학습 데이터를 이용해 모델을 구축한다. 분기하는 기준 변수 선정은 기본값으로 지니계수를 이용하는데 이번 예제에서는 엔트로피 계수(split = "information")로 변경하였다.
③ 구축된 의사결정나무 모델의 기본적인 정보를 확인한다.
아래 결과를 확인해보면 모델이 어떻게 분기되었고 최종 결과(리프)는 어떻게 되어 있는지 나온다.

그런데 텍스트로 나오므로 약간 직관적이지 않다. 모델에 대한 자세한 정보를 차트를 그려 살펴보자
library(rpart.plot) # 패키지가 필요하다
rpart.plot(iris.tree)
코드를 실행하면 <그림 1>과 같이 예쁜 차트가 그려진다. 우선 가장 상위 분기점에서 Petal.Length < 2.5 기준으로 데이터를 일차 분류하면 setosa의 경우 100% 분류할 수 있는 것으로 나온다(왼쪽 아래 빨간색 리프). 왼쪽 아래 빨간색 리프는 setosa, versicolor, virginica의 비율이 1.0, 0.0, 0.0 이고 전체 학습 데이터의 31%를 차지한다는 의미다.
의사결정트리 차트를 그리는 방법은 많은데, 다른 패키지(rattle)도 소개하고 넘어간다.
library(rattle)
fancyRpartPlot(iris.tree)
4. 모델 성능 평가
학습데이터로 만든 모델로 테스트 데이터를 분류해보고 모델의 성능 평가를 알아보자.
expect = predict(iris.tree,test[,-5],type = "class") #predict함수 이용, 범주이므로 type class 옵션
table(test[,5],expect) #예측값과 실제값 비교 테이블
코드를 실행하면 결과는 아래와 같다.

테이블에서 열은 예측이고 행은 실제 값이다. setosa 같은 경우 예측값이 17개이고 실제 값도 17개이므로 100% 정확하게 분류했다. 상대적으로 virginica의 경우 예측한 것 중에 9개만 정확했고 3개는 오분류했다는 것을 알 수 있다.
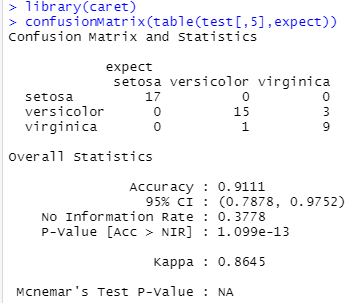
caret 패키지의 혼동행렬 함수를 이용하면 더 쉽게 모델의 성능을 평가할 수 있다. 실행해보면 정확도(accuracy)가 0.91정도 된다. recall, precision 등은 어떤 범주를 관심범주로 정할 것인가에 따라 달라지므로 여기에서는 생략한다.
library(caret)
confusionMatrix(table(test[,5],expect))
5. 앙상블 모델
실전에서는 하나의 나무모델만으로 분류 작업을 하는 경우는 드물다. 왜냐하면 의사결정나무는 상대적으로 과적합 경향이 다소 크기 때문이다. 아래 글에서는 의사결정나무의 단점을 보완하는 랜덤포레스트 모델에 대해 설명한다.
R 랜덤포레스트(randomforest)
관련글 R_의사결정나무 분석(rpart) 관련글 의사결정나무(decision tree) 관련글 선형회귀분석 밑바닥부터 이해하기 관련글 상관관계와 상관계수 상관관계와 상관계수 1. 들어가며 연속형 변수 x, y의
diseny.tistory.com
'R_데이터 분석 기술' 카테고리의 다른 글
| R 크론바흐 알파 값 계산 (0) | 2022.05.13 |
|---|---|
| R을 이용한 t-test와 효과 크기 계산 (0) | 2022.05.04 |
| R 랜덤포레스트(randomforest) (0) | 2022.05.03 |
| R 회귀분석 (0) | 2022.04.13 |
| R 교차표 작성 (0) | 2022.04.08 |
| R 주성분 분석 (0) | 2022.04.07 |
| R 다중공선성 VIF 값 계산 (0) | 2022.04.04 |




댓글