관련글
선형회귀분석 밑바닥부터 이해하기
관련글 상관관계와 상관계수 상관관계와 상관계수 1. 들어가며 연속형 변수 x, y의 관계는 상관관계(correlation) 분석을 통해 2가지 사실을 알 수 있다. 관계의 방향 관계의 강도 보통 관계의 방향은
diseny.tistory.com
1. 들어가며
선형회귀분석에서 모델의 적합도를 판단할 때, 결정계수(R^2)값이 중요한 판단 근거가 된다. 결정계수(R squared)의 의미에 대해 살펴보자.
2. 모델의 의미
예를 들어 <그림 1>과 같이 A ~ G(7명) 학생의 수학성적을 Y라고 했을 때 이 값들을 Y축 기준으로 나열해보자.
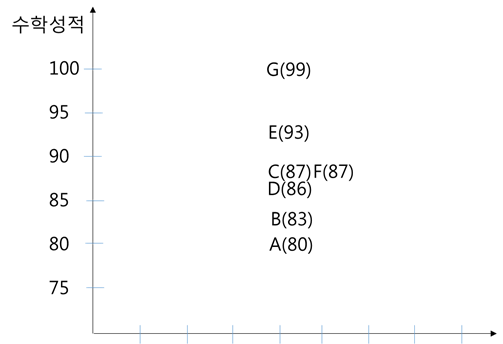
수학성적(Y)이라는 데이터를 이용해 구할 수 있는 것은 평균(88)과 표준편차(5.8)뿐이다. 그런데 각 학생들의 공부시간 데이터가 존재하고 이를 X라고 하자. 그런 다음에 X, Y의 관계를 2차원 평면에 그리면 <그림 2>와 같다.

이제 X와 Y의 관계를 설명할 수 있는 모델을 구축해보자. 가장 간단한 모델은 선형회귀모델이다. <그림 2>에 선형회귀 모델을 적합시킨 상태가 <그림 3>이다.

3. 결정계수의 의미
<그림 1>에서는 학생들의 수학성적에 차이가 있다는 사실은 알지만 왜 그런지 설명할 수 없었다. 그런데 X(공부시간) 데이터를 갖고와서 모델을 만들자 왜 학생들의 수학 성적에 차이가 나는지 설명할 수 있게 되었다.
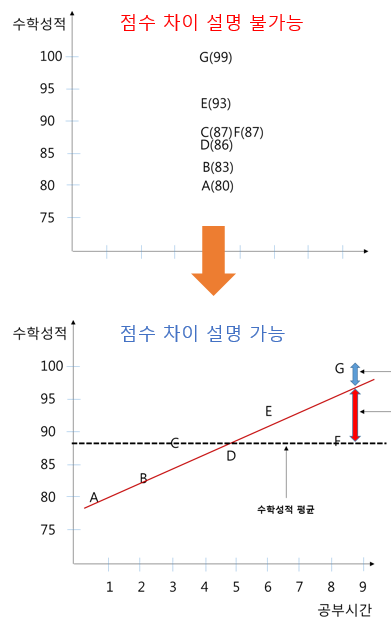
모델이 없던 위의 그림에서는 G학생의 점수(99점)가 왜 평균 점수(88점)보다 11점이나 높은지 모른다. 그런데 공부시간(X)이라는 데이터를 갖고와 모델을 만든 후, 그 모델을 이용해 G학생이 96점을 받은 이유까지는 설명할 수 있었다. 왜? 공부를 8시간 이상했으니까! 그런데 실제 점수는 99점이므로 나머지 3점은 모델을 이용해도 설명할 길이 없다.
결정계수는
G학생 99점 - 평균 88점 = 11점 (총 차이) ---①
회귀 모델로 설명이 되는
모델 예측 96점 - 평균 88점 = 8점 ------------②
①, ②비율을 의미한다. 모든 A ~ G 학생의 경우를 다 따져서 더하면 그 모델의 결정계수 값이 되는 것이다.
4. 결론
따라서 결정계수 값이 크면 그 모델로 개별 학생들의 점수 차이를 더 많이 설명할 수 있으니 모델의 적합도가 좋은 것이고 결정계수가 낮으면 모델이 있어봤자 점수 차이를 별로 설명하지 못하니 쓸모 없는 모델인 것이다.
'통계 이론' 카테고리의 다른 글
| 혼동행렬(confusion matrix) (2) | 2022.03.30 |
|---|---|
| 표준편차와 추론 통계 (0) | 2022.03.24 |
| ROC 곡선 아주 쉽게 이해하기 (2) | 2022.03.21 |
| 가설검증과 2종오류 (0) | 2022.03.06 |
| 분산으로 평균차이 검증하기(분산분석) (2) | 2022.03.02 |
| 가설검증과 1종 오류 (0) | 2022.02.24 |
| 다중공선성(Multicollinearity)의 의미와 판별법 (0) | 2022.02.16 |




댓글