1. 들어가며
통계 또는 머신러닝 모델을 만든 후에는 모델의 성능을 측정해야 한다. 대표적인 성능 측정 방법으로 혼동행렬과 ROC곡선이 있다. 혼동행렬표가 이해하기 쉬운데 반해 ROC 곡선은 직관적으로 이해하기에 다소 어렵다. ROC 곡선을 의미를 그림을 통해 쉽게 이해해보자.
※ 관련글 :
혼동행렬(confusion matrix)
1. 들어가며 이분형 예측 통계(머신러닝) 모델은 예측의 성능을 측정하는 기준이 필요하다. 이때 가장 대표적으로 이용되는 측정 지표가 혼동행렬표이다. 혼동행렬표로부터 모델의 성능을 측정
diseny.tistory.com
2. 전형적인 ROC 곡선
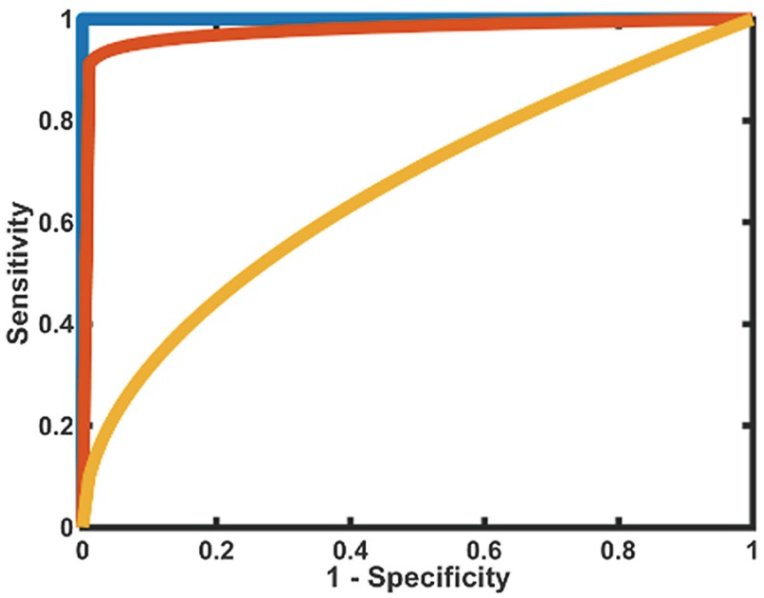
출처 : https://www.ncbi.nlm.nih.gov/books/NBK549564/figure/ch12.Fig6/
위의 <그림 1>은 전형적인 ROC 곡선인데, 일반적으로 파란색 > 빨간색 > 노란색 순으로 모델의 성능이 좋다고 배운다. <그림 1>을 이해하기 위해서는 X, Y축을 먼저 알아야 한다.
- Y축 = Sensitivity = 민감도
- X축 = 1- Specificity = 1 - 특이도
예를 들어 바이러스 검사를 통해 감염 유무를 예측(판정)하는 모델이 있다고 하자. 모델이 예측하는 것은 두 가지다.
- 감염된 사람을 감염자라고 판정
- 감염되지 않은 사람을 비감염이라고 판정
두 가지 범주 중에서 더 관심 있는 범주를 말 그대로 관심범주라고 한다. 위의 상황에서 감염자가 소수(minor)일텐데, 일반적으로 소수 범주을 예측하거나 판정하기 위해 모델을 만들기 마련이다.
민감도는 관심 범주를 제대로 예측한 정도를 의미하며 특이도는 관심범주가 아닌 대상을 제대로 예측한 정도를 의미한다. 위의 경우를 다시 쓰면 다음과 같을 것이다.
- 감염된 사람을 감염자라고 판정(민감도)
민감도 = 예측이 맞은 숫자 / 감염자라고 예측한 숫자 - 감염되지 않은 사람을 비감염이라고 판정(특이도)
특이도 = 예측이 맞은 숫자 / 비감염자라고 예측한 숫자
따라서 모델이 좋다고 말하려면 민감도와 특이도가 동시에 좋아야 하는데, 보통은 둘 중 하나의 성능이 상대적으로 낮은 경우가 많다.
3. 예측의 메커니즘 - 확률
범주를 예측하는 통계(머신러닝) 모델은 점술가처럼 범주를 정확하게 판단해주는 것이 아니라 단지 확률을 계산할 뿐이다. 즉, 데이터를 받아 분석한 결과 어떤 사람이 감염자일 확률 ~%, 또는 비감염자일 확률 ~%를 계산한다. 최종 판단은 분석가가 해야한다. 판단의 근거는 기준 확률이다. 대개는 50%를 기준으로 하고 이 값을 임계값 또는 경계값이라고 한다. 문제는 임계값에 따라 모델의 민감도와 특이도가 달라진다는 것이다.
4. 민감도와 특이도의 관계
아래 <그림 2>는 아주 좋은 모델인 경우이다. A 차트는 실제 데이터의 분포를 나타내는데 주황색(감염자 : 관심범주)과 검은색(비감염자)이 모델이 예측하는 확률 0.5를 기준으로 분명하게 나뉘어져 있다. 예측은 확률을 기준으로 판정하므로 0.5이상에 해당되는 주황색(실제 감염자)을 모두 감염자라고 판정할 것이고, 그 결과 민감도 =1, 확률 0.5 이하인 검은색은 모두 비감염자라고 예측할 것이므로 특이도 = 1 이다.
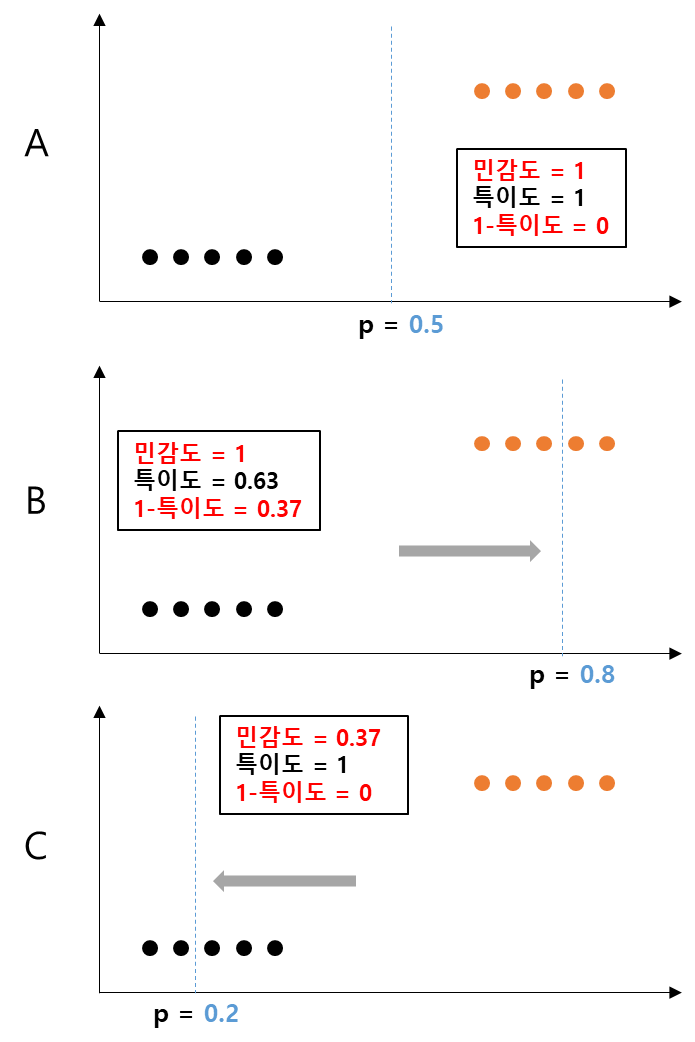
반면 B, C는 예측 임계값을 늘이거나 줄인경우인데 예를 들어 B의 경우 임계값을 0.8로 잡으면 0.8이하인 8개의 데이터(검은색 5개, 주황색3)를 모두 비감염자라고 예측할 것이다. 그러나 실제로 비감염자는 검은색 5개 이므로 특이도는 5/8 = 0.63이 된다. C는 반대의 경우다.
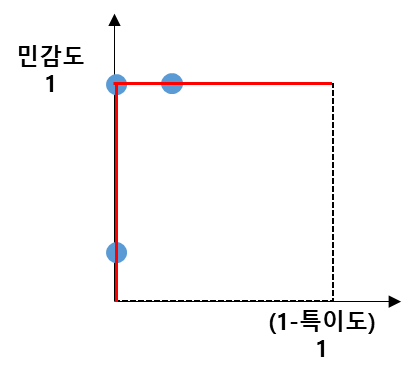
이렇게 A, B, C처럼 임계값을 변화시켜 민감도 VS (1-특이도) 쌍을 차트로 그린 것이 ROC곡선이다. <그림 3>을 보면 민감도 VS (1-특이도) 값이 빨간색 축에 붙어서 움직이는 것을 알 수 있다. 따라서 좋은 모델이 만들어 내는 ROC 곡선은 <그림 1>의 파란색 곡선처럼 만들어진다.
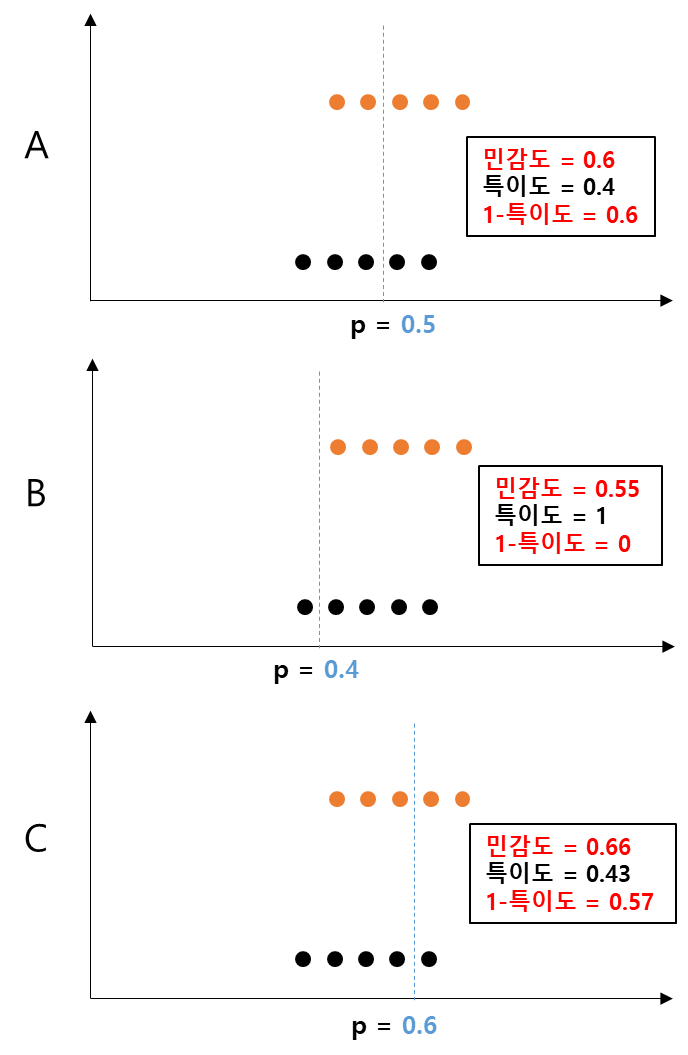
이제 <그림 4>는 다소 안 좋은 모델이다. 어떤 확률 임계점을 이용하더라도 실제값과 예측값이 정확하게 일치되기 어렵다. 이런 경우 A, B, C의 민감도 VS (1-특이도) 쌍 그래프를 그리면 <그림 3>과 같이 축에 바짝 붙어 있는 그래프가 아니라 축에서 멀리 떨어져 있는 그래프 모양이 된다.

5. 요약
ROC 곡선의 모양을 통해 모델의 성능을 시각적으로 판단할 수 있는데 정확한 수치가 필요할 때는 AUC(area under the ROC curve)값으로 구체적으로 나타낼 수 있다. AUC는 ROC 곡선의 면적을 의미한다. 당연히 좋은 모델의 ROC 곡선일 수록 면적이 크다.
관련글
혼동행렬(confusion matrix)
1. 들어가며 이분형 예측 통계(머신러닝) 모델은 예측의 성능을 측정하는 기준이 필요하다. 이때 가장 대표적으로 이용되는 측정 지표가 혼동행렬표이다. 혼동행렬표로부터 모델의 성능을 측정
diseny.tistory.com
'통계 이론' 카테고리의 다른 글
| 확인적 요인분석(CFA : Confirmatory Factor Analysis) (0) | 2022.03.30 |
|---|---|
| 혼동행렬(confusion matrix) (2) | 2022.03.30 |
| 표준편차와 추론 통계 (0) | 2022.03.24 |
| 결정계수(R^2)의 이해 (0) | 2022.03.08 |
| 가설검증과 2종오류 (0) | 2022.03.06 |
| 분산으로 평균차이 검증하기(분산분석) (2) | 2022.03.02 |
| 가설검증과 1종 오류 (0) | 2022.02.24 |




댓글