1. 기본 개념
QQ 플롯(Quantile-Quantile Plot)의 Quantile은 분위수라는 의미인데, 분위수는 데이터를 오름차순(내림차순)정렬한 뒤, 전체 데이터를 특정 개수로 나눌 때 기준이 되는 수다. 예를 들어 4분위수라고 하면 전체 데이터를 25%, 50%, 75%, 100%로 4등분한다는 것이다. 그렇다면 QQ 플롯을 말 그대로 표현하면 X, Y 축 척도가 분위수라는 의미인데, 개인적으로는 분위수 보다는 누적 분포 개념으로 생각하는 편이 QQ 플롯을 더 이해하기 쉽다고 생각한다.
2. QQ 플롯 활용
QQ 플롯은 보통 3가지 목적으로 이용된다.
- 주어진 데이터가 정규분포하는지 판단
- 주어진 두 세트의 데이터가 같은 분포인지 판단
- 회귀분석 등에서 잔차의 정규성 판단
그런데 사실 위의 3가지 목적은 표현 방식이 다르지 동일한 내용이다. 왜 그런지는 QQ 플롯을 그리는 원리를 알면 이해된다.
3. 전형적인 QQ 플롯
아래 그림은 구글에서 "QQ Plot" 키워드로 검색하면 발견할 수 있는 전형적인 그래프인데(Normal QQ plot), 필자가 추가 설명을 덧붙인 그림이다.
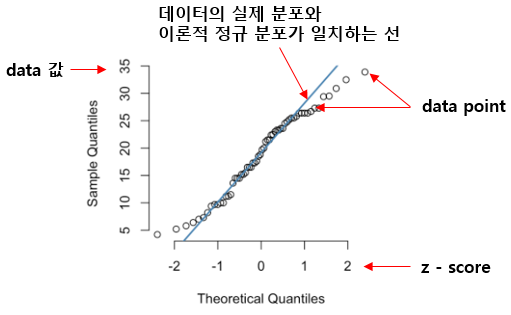
일반적으로 대각선위에 데이터 포인트가 놓여 있으면 정규 분포를 이룬다는 의미로 설명하는데 , 처음 QQ 플롯을 접하면 직관적으로 이해가 되지 않는다(개인적으로는 그랬음). X, Y축 스케일도 알쏭달쏭하고 책을 봐도 대각선과 데이터 포인트가 그려지는 원리에 대한 충분한 설명이 부족한 편이다.
4. QQ 플롯이 그려지는 원리
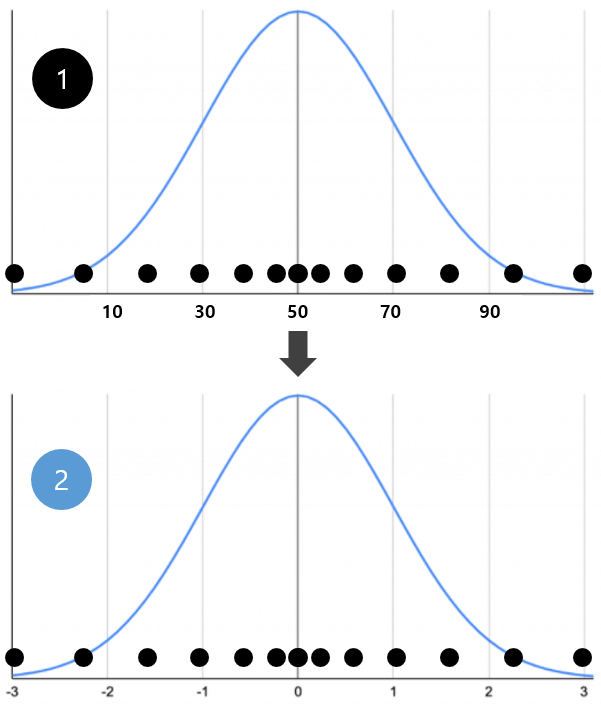
<그림 1>은 정규분포하는 ①번 데이터를 표준정규분포화(②)한 그림이다. 단순화시켜 표현한 이 그래프에서 눈여겨 보아야 할 것은 점으로 표현한 데이터의 배치간격이다. 데이터가 정규분포한다면 평균을 중심으로 밀집해 있어야 하고 양 끝으로 갈 수록 데이터가 드문드문 분포해야 할 것이며, 좌우대칭이어야 한다.
또한 ①번이 이론적으로 정규분포한다면 평균을 중심으로 퍼져있는 데이터 분포, 즉 간격이 표준화후 z 값의 분포와 일치할 것이다. 그렇다면 ①번 그래프의 X축을 Y축으로, ②번 그래프의 X축을 X축으로 하는 새로운 그래프를 생각해 보자.

<그림 2>는 데이터가 이론적으로 정규분포한다면 데이터를 표준화 후의 z 값과 매치 시키고 선을 그으면 45도 각의 선이 형성된다는 것을 의미한다. 만약 데이터가 정규분포하지 않는다면 어떻게 될까?
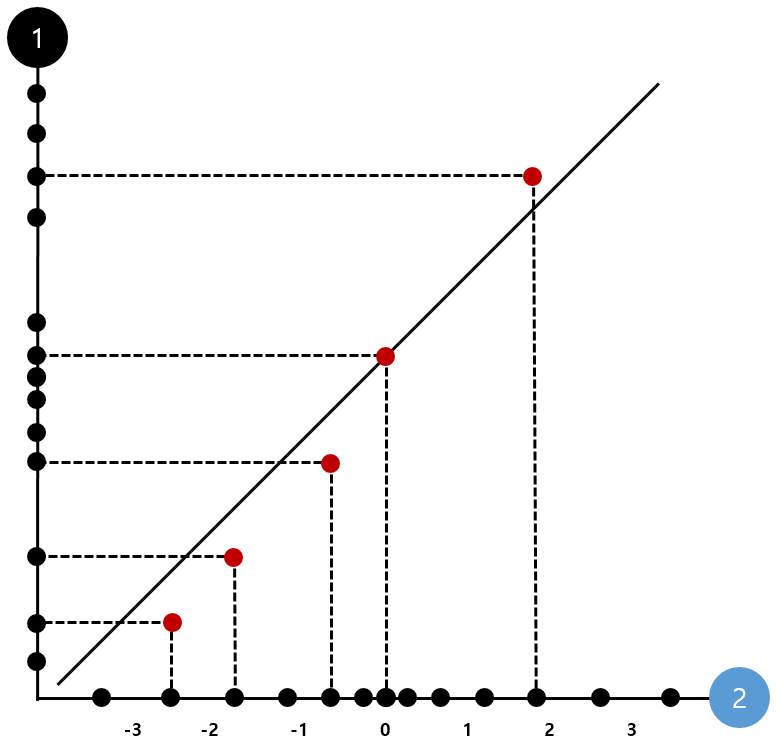
<그림 3>의 Y축은 더 이상 정규분포하지 않는다(간격 참고). 따라서 이론적으로 정규분포였다면 정확하게 매치되었을 대각선과 실제 데이터 포인트가 어긋나게 배치될 것이고, 얼마나 많이 어긋나는지에 따라 데이터의 정규성을 판단하면 된다. QQ 플롯은 정규성에 대한 정확한 수치값을 제시하는 것은 아니므로 대략적으로 판단할 때 사용한다.
A/B 테스트를 통한 통계적 사고 과정 따라가기
1. 들어가며추론 통계는 기술 통계에서 얻은 결과를 전체 모집단 차원으로 확대해서 그 결과를 일반화할 수 있는지 타진해보는 과정이다. 개인적으로 추론 통계의 핵심을 이해하는데는 두 집단
diseny.tistory.com
'통계 이론' 카테고리의 다른 글
| 자유도(Degree of Freedom)에서 자유로워 지기 (6) | 2022.02.06 |
|---|---|
| 제곱합(Sum of Squares : SS) 공식 (0) | 2022.02.01 |
| 다중회귀 분석에서 상호작용의 의미 (5) | 2022.01.31 |
| 도구의 신뢰도 측정(크론바흐 알파) (1) | 2022.01.26 |
| 탐색적 요인분석(EFA : Exploratory Factor Analysis) (0) | 2022.01.22 |
| 1. 5 데이터 과학 (0) | 2020.06.22 |
| 1.4 인공지능 (0) | 2020.06.22 |




댓글