※ 이전글
분산분석(ANOVA) 이해하는 가장 좋은 방법(1)
1. 들어가며 세 집단 이상의 비교에는 아노바(ANOVA)를 이용하는데 ANOVA는 Analysis of Variance의 줄임말이며 우리말로는 분산분석이다. 두 집단이든 세 집단이든 각 집단의 평균을 비교해 어디가 제일
diseny.tistory.com
1. 들어가며
(1)편에서는 논리적인 흐름을 깨지 않기 위해 그냥 분산이라고만 언급했지만 이제 집단간 분산과 집단내 분산을 구체적으로 계산해 보자. 계산 방법을 몰라도 분산분석의 대략적인 개념을 이해하는데는 문제가 없지만 데이터의 변동성을 정확하게 이해하는 것이 언제나 유익하다. 수식을 이해할 때는 아주 작은 규모의 데이터가 좋다. 아래 표는 A, B, C 세 집단이 각기 3개의 데이터를 갖고 있는 경우이다.
| No | A | B | C |
| 1 | 2 | 2 | 6 |
| 2 | 3 | 3 | 7 |
| 3 | 4 | 3 | 8 |
| 평균 | 3 | 2.7 | 7 |
2. 총변동성
위의 데이터를 집단 정보(A, B, C)가 없다고 생각하고 하나의 데이터로 생각하자.
그러면 데이터 X = { 2, 3, 4, 2, 3, 3, 6, 7, 8}이다.
데이터의 평균은 소수점 둘째 자리에서 반올림해서 4.2이다. 이제 이 총평균을 이용해서 데이터의 총 변동성을 구해보자.
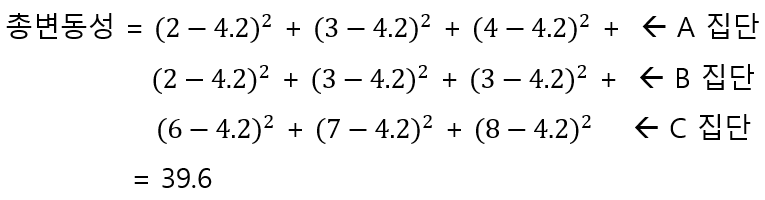
총 변동성은 제곱합 공식을 이용해 더 간단하게 구할 수 있다. 평균이 소수점 숫자까지 나올 때는 제곱합 공식을 이용해 평균을 사용하지 않고 계산할 수 있어 더 편리하다.

위의 제곱합 공식에 대한 내용은 아래 관련글을 참고하기 바란다.
제곱합(Sum of Squares : SS) 공식
1. 기본개념 X = { x1 , x2 , ………, xn } 일 때 , 데이터 X의 분산을 구하는 공식은 다음과 같다. 중학교(고등학교?)에서 배우는 식이다. 위의 식에서 분자 부분을 제곱합(Sum of Squares : SS)이라고 부
diseny.tistory.com
3. 집단내 변동성
위의 데이터에서 집단내 변동성은 말 그대로 개별 집단의 데이터에 각 집단의 평균을 빼고 제곱한 값의 합이다.

집단내 변동성 = A집단내 변동성 + B집단내 변동성 + C집단내 변동성 = 2 + 0.3 + 2 = 4.3
4. 집단간 변동성
이제 집단간 변동성을 계산해보자. 총 변동성과 집단내 변동성을 계산하는 방법은 직관적으로 이해하기 쉬운데 집단간 변동성은 약간 생각을 해야한다. 아래 과정은 집단간 변동성을 계산하는 방법이다. 총 변동성을 계산할 때와 비슷하지만 식에 개별 데이터 대신 각 집단의 평균 값이 대입되었다는 사실에 유의하기 바란다.

이 식은 집단내에서 발생하는 개별 데이터의 변동성은 무시하고 각 집단의 표준적인 값, 즉 대표하는 값으로 총변동성에서 집단 효과를 분리해내겠다는 의미다.
예를 들어 한국인과 미국인의 키 차이에 대한 변동성을 계산한다면 총 변동성에는 개인의 특성(유전적 성격)에 따른 키 차이와 한국인, 미국인이라는 집단 특성 때문에 발생하는 키 차이가 섞여 있다. 즉 내가 175cm인 이유는 유전, 혹은 환경 같은 개인적 이유와 한국인이라는 집단적 이유가 섞여 있는 것이다.
그런데 한국인 평균키, 미국인 평균키를 이용해 변동성을 계산하면 그 값에는 개인의 특성, 즉 한국인 집단내의 특성, 미국인 집단내의 특성은 제거되고 오직 집단의 특성만 남게 되는 것이다. 이를 증명하는 수식이 아래와 같다.
총 변동성(39.6) = 집단내 변동성(4.3) + 집단간 변동성(34.6)
그런데 지금까지 구한 것은 변동성이지 분산은 아니다. 분산은 변동성의 평균이다. F값 공식에는 변동성이 아니라 분산을 대입해야 한다.

지금까지 계산해 온 과정의 목적은 통계적 유의성을 검증하는 것이다. 즉 모집단에서의 적용 가능성을 따지는 것이므로 여기에서 말하는 분산도 모집단의 분산을 추정한 불편분산입니다. 따라서 분산(변동성의 평균)을 구할 때 분모에 자유도를 사용한다.
자유도(Degree of Freedom)에서 자유로워 지기
1. 들어가며 자유도는 통계학을 공부하다 보면 아마 제일 처음 만나는 알쏭달쏭한 개념이다. 최초로 등장하는 시기는 표본분산을 구할 때다. 표본으로 모분산을 추정할 때는 표본의 개수(n)가 아
diseny.tistory.com
집단내 변동성을 구할 때 자유롭게 선택할 수 있는 표본은 전체 표본의 개수 9개 중에 6개이다. A집단내 변동성을 구할 때 2개까지는 자유롭지만 마지막 하나는 A집단 표본평균이 이미 정해져 있기 때문에 마지막 표본은 고정되어야 한다. B, C 집단도 마찬가지이므로 2 X 3 = 6이다. 집단간 변동성을 구할 때는 식에서 집단의 평균 표본 3개 중에서 2개만 자유롭게 선택가능하고 마지막 하나의 표본 평균은 고정이다. 그래서 자유도는 3-1 = 2 이다.
자유도는 총변동성과 동일한 논리가 성립한다.
총 자유도(9-1) = 집단내 분산 자유도(9-3) + 집단간 분산 자유도(3-1)
이제 자유도까지 구했으므로 지금까지 구한 값을 F공식에 대입하자

F = 24.7 이라는 값의 의미는 집단내에서 우연하게 발생할 수 있는 분산보다 집단간의 분산이 24.7배가 더 크다는 말이며 일부 집단 또는 각 집단이 서로 달라서 집단간의 분산이 매우 크다는 사실을 말해준다.
5. 통계적 유의성
A, B, C의 모집단 평균이 동일하다면 이 표본 집단간의 변동성이 클 수 없을 것이고 따라서 F값은 작아야 한다. 그런데 예제에서는 24.7이라는 값이 나왔고 만약 A, B, C가 동일한 모집단이라고 가정했을 때 F가 24.7 이상이 나올 확률은 아주 작을 것이다. 결론적으로 A, B, C의 평균이 동일하다는 가정을 기각하고 모집단 수준에서 집단간 분산이 크다, 즉 어느 한 집단이 다르거나 집단끼리 다르다고 말할 수 있다.
6. 효과크기
t-test와 마찬가지로 효과 크기가 중요하다. 분산분석에서 효과 크기는 η2 (에타제곱)이라고 하고 회귀 분석의 R2 과 유사하다.
η2 = 집단간 변동성총 / 변동성 = 집단간 변동성 / (집단간 변동성 + 집단내 변동성)
위 식은 데이터의 총 변동성 중에서 얼마나 많은 변동성이 집단의 차이에서 비롯되었는지 측정한다. η2 (에타제곱) 값이 1보다 클 수 없으므로 최대 값은 1이며 값이 클수록 집단이 다름으로 인해 발생하는 차이가 크다는 의미다. 이번 사례에서는 0.89이다.
η2 = 34.6 / (34.6 + 4.3) = 0.89
7. 사후검증
F값 공식에서는 식 어디에도 A, B, C 중 어떤 집단이 어떤 집단보다 평균이 크거나 작다는 정보는 찾을 수는 없다. 단지 집단간 분산이 크다 작다만 말해줄 뿐이다. 따라서 집단간 차이가 있다는 것을 발견했다면 구체적으로 어떤 집단이 차이가 있는지를 확인해야 한다. 이를 사후 검정이라고 한다.
사후 검증 방법은 단순하다. A : B, A : C, B : C로 짝을 지어 평균 차이를 비교하고 통계적 유의성을 검증한다(t-test). 그런데 앞에서 이런 방법은 오류 가능성이 5%를 넘기 때문에 사용하지 않는다고 설명했다. 집단 별 검정 횟수가 늘어나면 오류 가능성도 계속 누적이 되므로 단순하게 총 누적 오류가 5%를 넘지 않도록 통계적 유의성 판정 기준을 더 낮도록 정한다. 이런 방식을 본페로니(Bonferroni) 방법이라고 한다.
다음글에서는 집단에 하위 분류가 있는, 즉 이원분산분석(two way anova) 계산방법에 대해 알아보자.
분산분석(ANOVA) 이해하는 가장 좋은 방법(3)
1. 들어가며 이전글은 세 집단의 차이를 비교하는 일원분산분석(one way anova)을 설명했다. 분산분석(ANOVA) 이해하는 가장 좋은 방법(2) ※ 이전글 분산분석(ANOVA) 이해하는 가장 좋은 방법(1) 1. 들어
diseny.tistory.com
Reference
1. Statistics for the Behavioral Sciences, Frederick J Graveltter, Larry B. Wallnau
2. Collaborative Statistics, Barbara Illowsky, Susan Dean.
'통계 이론' 카테고리의 다른 글
| 로지스틱회귀와 친구되기(2) (0) | 2022.04.26 |
|---|---|
| 로지스틱회귀와 친구되기(1) (0) | 2022.04.26 |
| 분산분석(ANOVA) 이해하는 가장 좋은 방법(3) (0) | 2022.04.25 |
| 분산분석(ANOVA) 이해하는 가장 좋은 방법(1) (4) | 2022.04.22 |
| t-test 밑바닥부터 이해하기 (4) | 2022.04.21 |
| F분포 어디에 쓰일까? (5) | 2022.04.21 |
| 카이제곱 분포 이해하기 (4) | 2022.04.19 |




댓글