1. 들어가며
연속형 변수 x, y의 관계는 상관관계(correlation) 분석을 통해 2가지 사실을 알 수 있다.
- 관계의 방향
- 관계의 강도
보통 관계의 방향은 그래프를 그려 확인하고, 관계의 강도는 그래프로도 확인 가능하지만 구체적인 값을 계산한다. 관계의 방향과 강도를 파악하는 방법에 대해 살펴보자.
2. 관계의 방향
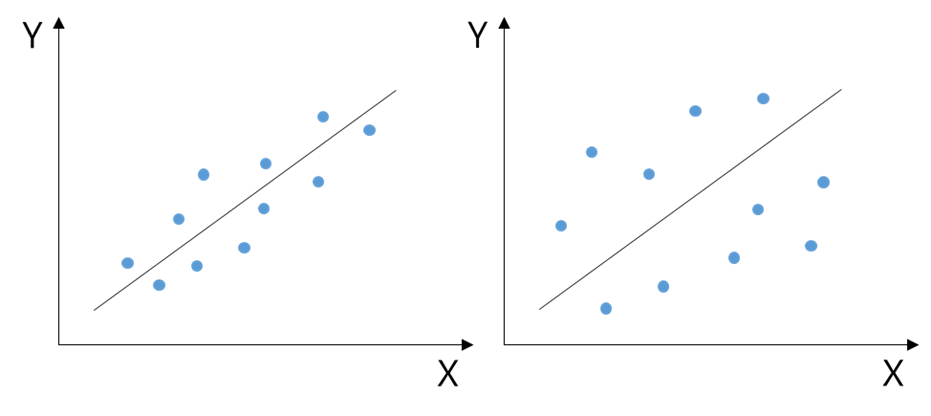
관계의 방향은 3가지 경우로 나뉜다. <그림 1>은 일반적인 3가지 경우의 관계를 나타내고 있다. 산점도를 그리고 추세선을 그어보면 대략의 방향성이 나오는데 제일 왼쪽 그래프는 x, y가 양의 상관관계(postive), 두 번째 그래프는 x, y가 음의 상관관계(negative), 제일 오른쪽 그래프는 x, y가 아무런 상관성이 없다는 의미다.

3. 관계의 강도
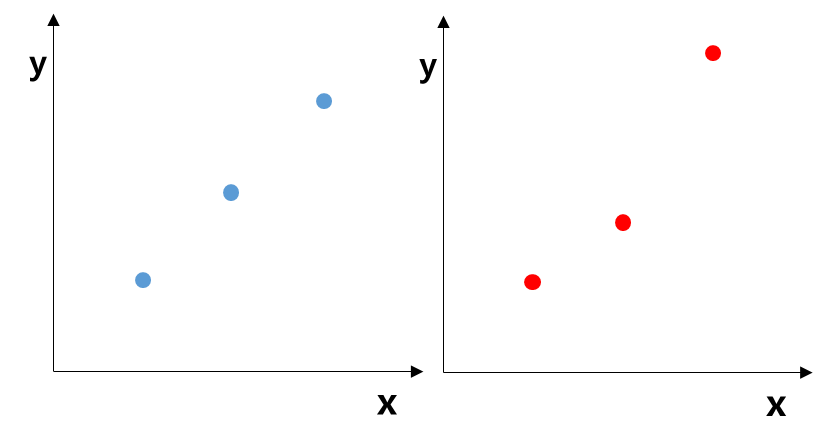
관계의 방향성을 알았다면 어느 정도 관계가 강한지 알아야 한다. 아래 <그림 2>는 두 종류의 X, Y 관계를 나타낸 그래프다. 두 그래프 모두 x, y에 양의 상관관계가 있다는 것을 알 수 있다. 그렇다면 어느 쪽의 상관관계가 더 강할까?
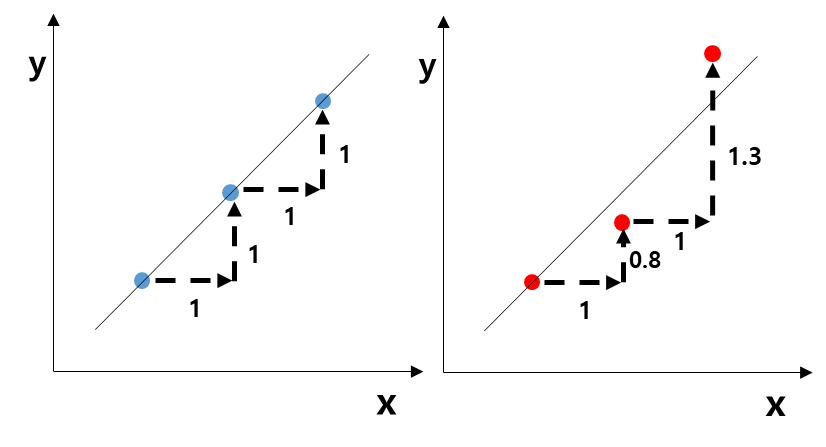
<그림 2>를 <그림 3>처럼 다시 그려보자. 왼쪽 파란색 그래프에서는 x, y의 변화량이 같다. 즉 x가 1 움직이면 y도 1 움직인다. 반면 오른쪽 빨간색 그래프에서는 x가 증가하면 y도 증가하지만 그 양이 일정하지가 않다. 따라서 x, y의 움직임 양이 동일한 왼쪽 그래프에서의 x, y 상관관계가 더 강하다.
<그림 3>을 더 많은 데이터를 포함하는 일반적인 산점도로 나타내면 <그림 4>와 같다.
4. 관계의 강도를 값으로 나타내기 : 공분산
그런데 그래프로만 두 변수 x, y의 관계 강도를 나타낼 수는 없다. 객관적인 수치가 필요하다. 이를 위해 필요한 개념이 공분산(covariance)이다. 공분산은 데이터가 각 변수의 평균과 어떤 방향으로 얼마나 떨어져 있는지 계산한 값으로서 공분산의 절대값이 두 변수의 관계 강도를 나타낸다. 구체적인 사례로 이해해 보자.
| No | X | Y | Z |
| 1 | 1 | 4 | 4 |
| 2 | 3 | 7 | 2 |
| 3 | 5 | 4 | 7 |
| 4 | 7 | 8 | 3 |
| 평균(mean) | 4 | 5.75 | 4 |
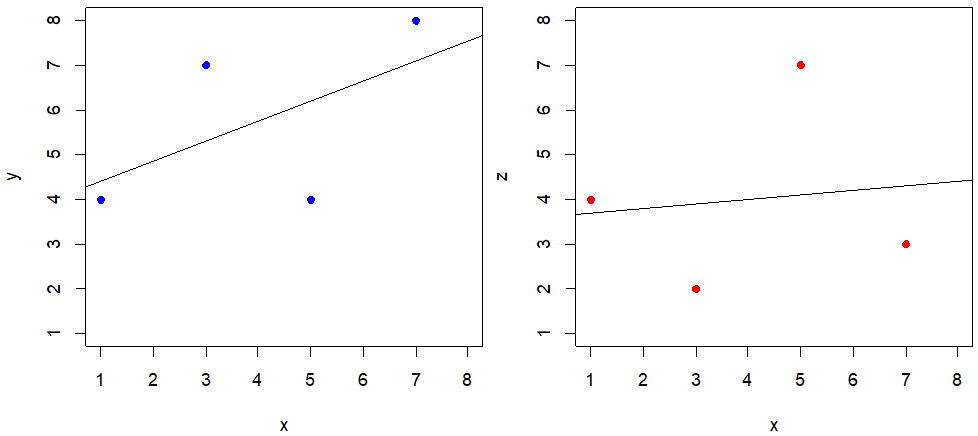
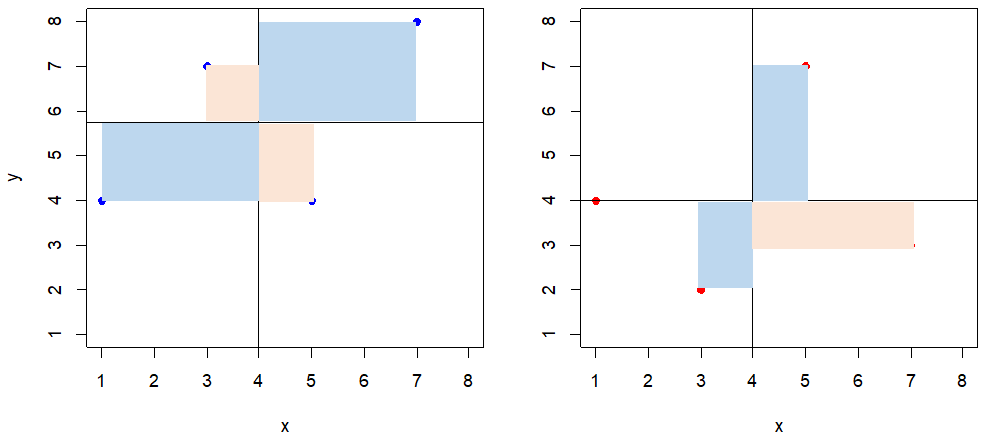
위 테이블의 데이터에서 x, y 관계와 x, z 관계를 그래프로 그려보면 아래 <그림 5>와 같다. 그림으로 보면 왼쪽의 x,y 관계 강도가 더 강한 것 처럼 보이긴 하지만 확실하지 않다. 그래서 우리는 공분산을 구해야 한다.
- x, y 공분산 = (1-4)(4-5.75) + (3-4)(7-5.75) + (5-4)(4-5.75) + (7-4)(8-5.75)
- x, z 공분산 = (1-4)(4-4) + (3-4)(2-4) + (5-4)(7-4) + (7-4)(3-4)
위의 공분산을 구하는 방법을 그림으로 나타내 보자. 양 그래프에서 가로 , 세로 축은 각각 x, y, z 축의 평균이고 색이 칠해진 사각형 영역은 공분산 계산에서 하나의 항을 의미한다. 예를 들어 x, y 공분산 계산 식에서 첫번째 항(1-4)(4-5.75)은 아래 <그림 6> 왼쪽 그래프에서 하나의 파란색 직사각형을 의미한다. 파란색 사각형은 (+)값, 분홍색 사각형은 (-) 값을 의미한다. 따라서 각 그래프의 사각형 면적을 다 더하면 공분산 값이 되며 이 값으로 양 그래프를 비교해 어느 쪽 값이 더 큰지를 보면 된다.
5. 피어슨 상관계수
공분산은 관계의 강도를 구체적인 수치로 나타내기에 좋은 값이지만 치명적인 단점은 데이터의 단위에 따라 값이 달라져서 만약 x, y, z의 단위가 다르다면 이번 경우처럼 공분산으로 (x, y) VS (x, z) 를 비교할 수 없다는 것이다. 이를 보완하기 위해 공분산을 각 변수의 표준편차로 나눠주면 피어슨 상관계수(r) 값을 얻을 수 있다.
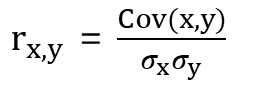
상관계수(r)는 -1에서 1사이의 값을 가지며 1에 가까울 수록 양의 관계가 강하고, -1에 가까울 수록 음의 관계가 강하며 0에 가까우면 아무런 관계가 없다는 것을 의미한다. 수식의 의미를 말로 풀어 설명하면, X가 1 표준편차만큼 변할 때 Y는 얼마나 변하는가를 나타낸다. 따라서 상관계수가 1이면 둘이 완벽하게 같은 양만큼 변하고 0에 가까우면 X가 변해도 Y는 변하지 않는다는 의미다. 반대로 Y 기준으로 생각해도 동일하다.
피어슨 상관계수가 절대적으로 얼마가 되면 두 변수의 상관관계가 크다고 말할 수 있을까? 논문을 쓸 때는 0.6이상이면 비교적 큰 상관계수라고 받아들이지만 실제 데이터 분석을 해보면 0.6이상의 값을 얻기가 쉽지는 않다.
6. 요약 및 결론
두 변수 x, y의 관계는 관계의 방향성(양, 음, 없음)과 관계의 강도를 분석할 수 있고 그래프를 그려 관계의 방향성과 강도를 직관적으로 알 수는 있지만 구체적인 크기에 대한 평가를 위해 피어슨 상관계수를 계산해야 한다. 피어슨 상관계수는 데이터 변수의 단위와 무관하게 관계의 절대적인 크기를 가늠할 수 있다.
결정계수(R^2)의 이해
1. 들어가며 선형회귀분석에서 모델의 적합도를 판단할 때, 결정계수(R^2)값이 중요한 판단 근거가 된다. 결정계수(R squared)의 의미에 대해 살펴보자. 2. 모델의 의미 예를 들어 <그림 1>과 같이 A ~ G
diseny.tistory.com
R을 이용해 상관계수 구하기
관련글 상관관계와 상관계수 1. 들어가며 상관계수의 개념에 대해서는 관련글을 참고하기 바란다. 이제 R을 이용해 상관계수를 구하고 간단하게 시각화하는 방법을 정리해보자. 피어슨 상관계
diseny.tistory.com
상관계수의 크기에 대한 감 잡기
상관관계와 상관계수 1. 들어가며 연속형 변수 x, y의 관계는 상관관계(correlation) 분석을 통해 2가지 사실을 알 수 있다. 관계의 방향 관계의 강도 보통 관계의 방향은 그래프를 그려 확인하고, 관
diseny.tistory.com
'통계 이론' 카테고리의 다른 글
| 이상값과 영향력 있는 관측값 탐지 (2) | 2022.04.14 |
|---|---|
| 회귀진단 (0) | 2022.04.13 |
| 선형회귀분석 밑바닥부터 이해하기 (0) | 2022.04.01 |
| 확인적 요인분석(CFA : Confirmatory Factor Analysis) (0) | 2022.03.30 |
| 혼동행렬(confusion matrix) (2) | 2022.03.30 |
| 표준편차와 추론 통계 (0) | 2022.03.24 |
| ROC 곡선 아주 쉽게 이해하기 (4) | 2022.03.21 |




댓글