관련글
1. 문항반응이론(IRT) 개요
1. 기본개념 문항반응이론(Item Resposne Theory)은 여러 사람들이 여러 문항에 응답한 데이터를 분석해 응답자의 능력 개별 문항(문제)의 난이도/변별력/추측도 를 측정하는 분석 이론이다. 문항(item)
diseny.tistory.com
2. 이분형 문항 반응 특성 곡선 원리
이전글 : 1. 문항반응이론개요 1. 들어가며 이분형 문항 반응(dichotomous response)이란 문제(문항)에 대한 응답 범주가 2가지라는 의미다. 어떤 문제의 정오답 데이터가 전형적인 이분형 문항 반응이
diseny.tistory.com
1. 필요 패키지
IRT를 분석하는 R 패키지는 아주 많지만 일반적으로 많이 쓰이는 패키지는 ltm, mirt 두 가지다. mirt는 단일차원성(unidimensionality)뿐만 아니라 다차원성(multidimensionality) 데이터 까지 분석하므로 ltm 패키지 보다 기능적으로 더 확장되어있다. 본 포스팅은 mirt 패키지 기준으로 설명한다.
2. 데이터 생성
0 또는 1로 구성된 임의의 랜덤 데이터를 100개 만들어, 10 X 5 행렬 데이터를 만든다. 각 행은 수험자이고 각 열은 문항이 될 것이다. 코드는 아래와 같다.
set.seed(123) #(1)
s_score = matrix(rbinom(100,1,0.5), nrow = 20) #(2)
s_score = as.data.frame(s_score) #(3)
names(s_score)=c(1,2,3,4,5) #(4) 데이터 프레임의 열에 이름을 붙임
head(s_score)#(1) 랜덤 생성 데이터가 일정하게 나오도록 랜덤 시드 고정
#(2) 바이너리(0 or1) 데이터를 100개 만들어서 20행 매트릭스 데이터 생성
#(3) 매트릭스 데이터를 데이터 프레임으로 변환
#(4) 데이터 프레임의 열에 이름을 붙임
코드를 실행하면 컴퓨터마다 다른 결과가 나올 것이다. 그러나 기본적으로 비슷한 성질의 데이터가 만들어 진다. 이제 이 데이터의 행이 수험자(20명) 열이 문제(5개), 0은 틀림, 1은 맞음이라고 정의하자.

3. 1PL 모델 구축
이분형 IRT 모델은 1PL, 2PL, 3PL이 있다. 이와 관련해서는 위의 관련 글을 참고하기 바란다. 여기에서는 오직 난이도만 추정하는 1PL 모델을 구축해본다. 일반적으로 1PL 모델을 Rasch 모델이라고 부른다.
library(mirt) #패키지 로드
one_m <- (mirt(s_score, model=1, itemtype = 'Rasch', SE = T))
one_m아래는 모델에 대한 정보이다.

4. 모델 결과 분석
코드를 실행하면 아무일 없이 끝난다. 이제 하나씩 결과를 보자.
(1) 문항 모수 : 문항(item)별 난이도
# one_m 은 위에서 구축한 모델 객체이다
coef(one_m, IRTpars=T, simplify=T)결과는 다음과 같다.

a는 변별도인데 1PL모델이므로 동일하다. b가 난이도인데 2번 문제가 가장 쉬운 것으로 나타났다.
(2) 수험자 능력 추정 : 20명의 피험자 능력치 추정 값
fscores(one_m, method = "MAP", full.scores = T, full.scores.SE = T)결과는 다음과 같다.

편의상 8번 수험자까지 표시했다. 7,8번 수험자의 능력이 상대적으로 뛰어남을 알 수 있다.
(3) 문항특성곡선(ICC)
다섯 문항의 특징을 그려보자. 랜덤 데이터이므로 거의 비슷한 모양의 그래프를 얻을 것이다.
plot(one_m, type="trace")결과는 아래와 같다.

(4)테스트 정보 함수
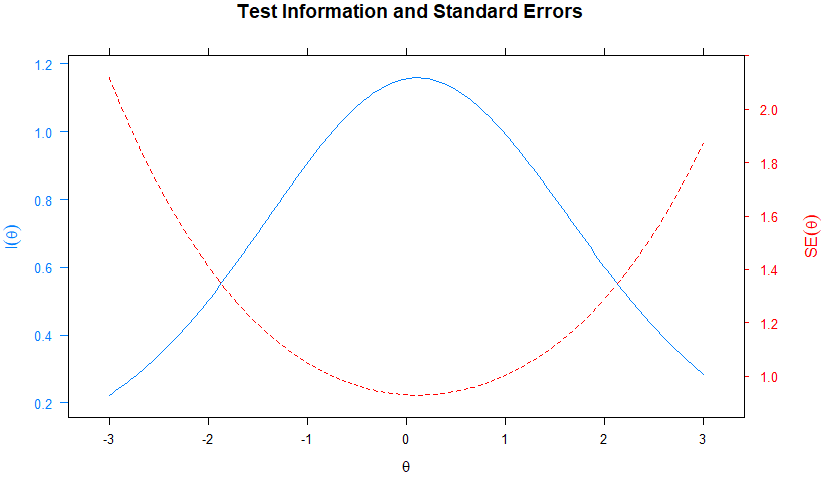
5개로 구성된 이 테스트가 어떤 범위의 능력치에 있는 수험자를 가장 가려내는지에 대해 알려준다.
#능력치 -3 ~ 3 사이만 그래프로 나타냄
plot(one_m, type ='infoSE', theta_lim = c(-3, 3))결과는 다음과 같다. 파란색 그래프가 정보함수인데 능력치 0(중간)에서 가장 값이 크다. 즉 능력치가 중간인 수험자의 능력을 잘 판별하는 테스트라는 것을 나타낸다.
다음글
4. 이분형(dichotomous) 문항 2PL, 3PL 모델 분석
이전글 3. R_이분형(dichotomous) 문항 1PL 모델 분석 1. 들어가며 지난 글에서 문항의 난이도만 추정하는 1PL 모델 분석을 방법을 다뤘다. 이제 문항의 변별도를 모델에 포함시키는 2PL모델과 추측도까
diseny.tistory.com
'문항반응이론(IRT)' 카테고리의 다른 글
| 5. IRT 모델 진단 (0) | 2022.03.07 |
|---|---|
| 4. 이분형(dichotomous) 문항 2PL, 3PL 모델 분석 (0) | 2022.03.07 |
| 2. 이분형 문항 반응 특성 곡선 원리 (0) | 2022.01.24 |
| 1. 문항반응이론(IRT) 개요 (0) | 2021.04.19 |




댓글